Primary students (K-2): geometry, counting, repeated addition
Intermediate students (3-5): geometry, single- and double-digit multiplication, distributive property of multiplication, array model of multiplication
What's really cool about multiplication is that no matter what two numbers are multiplied together, geometrically the result creates a rectangular array*. That's because multiplication is simply repeated addition. The color coding of the poster array helps students visualize this repeated addition. For example, the pink rectangle represents 3 + 3 + 3 + 3 + 3 and so on. But equally clear is that the problem 14 x 13 is 14 rows of 13: 13 + 13 + 13 + 13 + 13...
The other really cool thing is that we can break that visual representation down into partial products. For example, the array on the poster represents the problem 14 x 13. Using partial products to solve the problem would look like: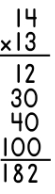
Each one of the partial products is clearly visible in the array model. When we break apart the factors into addends (10 + 4 and 10 + 3) and then multiply, we're using the distributive property of multiplication.
This array is a great example of how the different topics in math can help support each other...in our case how geometry can show how numbers work.
*A rectangular array is made up of squares laid out in rows and columns.
"I noticed it's a 13x14. I also noticed 100 blue squares, 30 pink squares, 12 yellow squares, and 40 green squares."
"There are lots of squares - 11."
"I notice 100 blue, 30 pink, 40 green, 12 yellow: 100+30+40+12=182 total colors (colored squares)"
"I notice it is 10x16, 4x10, 3x10, 4x3."