Primary students (K-2): shapes, number recognition, counting, relative sizes
Intermediate students (3-5): multiplication, area, pattern
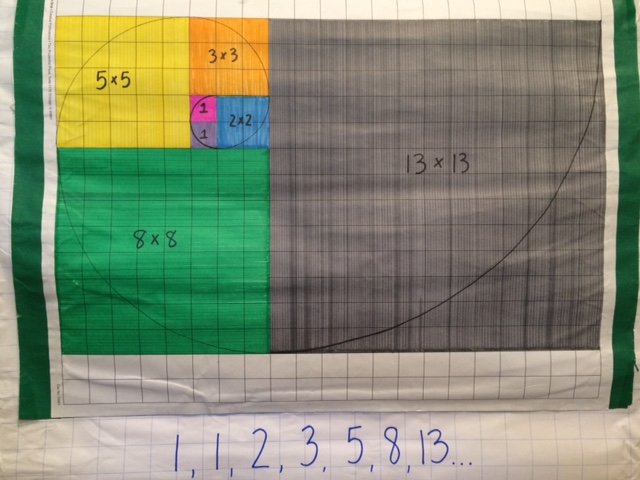
Fibonacci numbers are a series of numbers where a number is found by adding up the two numbers before it. Starting with 0 and 1, the sequence goes 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. At a very high level, the pattern of numbers creates the rule: xn = xn-1 + xn-2.
Fibonacci numbers are prevalent in nature in the form of spirals in sunflowers, hurricanes, and galaxies. They can also be found in the spiral of the nautilus shell. A visual example of this is seen in the graphic on the poster. The Fibonacci spiral can be made by creating squares with the dimensions of the Fibonacci numbers then connecting quarter circles within those squares. The Fibonnaci numbers have a ratio close to the Golden Ratio, 1.618034 and the spiral and resulting rectangle are known as the Golden Rectangle.
Another way to display this poster would be to remove the multiplication expressions. That way, students can make the connection between the Fibonacci sequence of numbers and the successively larger rectangles.
Here is a link to how I taught this as an art project.