Primary students (K-2): number recognition, counting, pattern, addition, geometry
Intermediate students (3-5): addition, even numbers, geometry
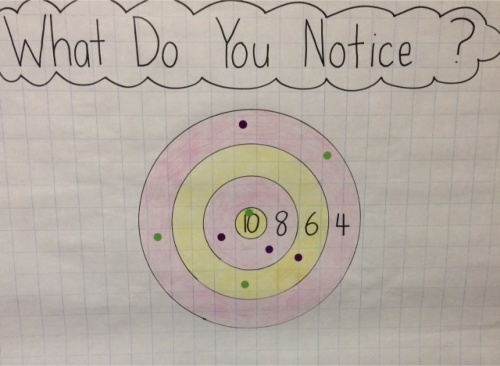
The idea to do something with a target came to me when I was watching the World Curling Championships. Although the sport of curling doesn’t use number values for each of the rings, it reminded me of archery targets which do have number values, although not necessarily indicated on the target itself.
So I designed my target with the number values 4, 6, 8, and 10 for the bullseye. Then I added 4 each of purple and green "dots" (stickers).
Younger students might count the number of green dots and purple dots and find that each color has the same number of dots. They might count the number of circles/rings and notice a repeating color pattern: yellow, pink, yellow, pink. They may also recognize and read the numbers 10, 8, 6, 4.
One of the first things all students will probably notice is that the target is made up of circles. These are actually concentric circles – circles that have a common center.
At a higher level, students may notice that the numbers on the target are all (consecutive) even numbers. They may determine which color, purple or green, had the highest score by adding the numbers. A question that could be asked is, “Would it be possible for anyone using this target to get an odd-numbered score? Why or why not?” Of course, when adding even numbers only, an odd sum is not possible.
Designing your target: To make the target, you’re going to need to draw concentric circles. Because the outer ring was larger than my compass would allow, I used a technique I’ve done with students where they create their own tool to help with the drawing of circles. The photo below shows the tool I made and here’s a link to a video I put together with step-by-step directions on how to make it.
For my target I chose to make the ring widths 1 ½ inches. That way it wouldn’t take up too much space on the chart paper but still be large enough to see from a distance of a few feet. In order to make the bullseye, I had to determine half of 1 ½ because that represents the radius of that center circle. I used number sense to help: half of 1 is ½. And half of ½ is ¼. Therefore, ½ + ¼ = ¾” radius.

"All the numbers are even"
"There are 4 green stickers and 4 purple stickers."
"They are all even; they all add 2; the dots add up to 50."
"Counting by 2 back from 10 to 4."